AMC數(shù)學(xué)競(jìng)賽是什么？AMC數(shù)學(xué)競(jìng)賽難嗎？AMC數(shù)學(xué)競(jìng)賽適合幾年級(jí)學(xué)生？如何備考AMC數(shù)學(xué)競(jìng)賽？有沒(méi)有AMC數(shù)學(xué)競(jìng)賽的歷年真題？AMC數(shù)學(xué)競(jìng)賽考試內(nèi)容有嗎？考試大綱有沒(méi)有？要怎么備考AMC數(shù)學(xué)競(jìng)賽?
AMC數(shù)學(xué)競(jìng)賽介紹
美國(guó)數(shù)學(xué)競(jìng)賽AMC是由美國(guó)數(shù)學(xué)協(xié)會(huì)MAA主辦的美國(guó)國(guó)家級(jí)蕞重要的系列數(shù)學(xué)競(jìng)賽，由美國(guó)數(shù)學(xué)協(xié)會(huì)主辦，是美國(guó)國(guó)家級(jí)別的系列數(shù)學(xué)競(jìng)賽。這項(xiàng)競(jìng)賽是為所有喜愛(ài)數(shù)學(xué)的學(xué)生所開(kāi)發(fā)的，試題由簡(jiǎn)至難兼具，使任何程度的學(xué)生都能感受到參與競(jìng)賽的挑戰(zhàn)，同時(shí)，賽程設(shè)置還可以篩選出在數(shù)學(xué)領(lǐng)域別具天賦的選手。對(duì)于想要申請(qǐng)理工科專(zhuān)業(yè)的學(xué)生來(lái)說(shuō)，AMC競(jìng)賽能夠極大提升大學(xué)的申請(qǐng)競(jìng)爭(zhēng)力。如斯坦福、麻省理工、加州理工等名校都會(huì)把AMC成績(jī)作為錄取學(xué)生的重要指標(biāo)。AMC也是美國(guó)中學(xué)校長(zhǎng)每年重點(diǎn)推薦的活動(dòng)之一。
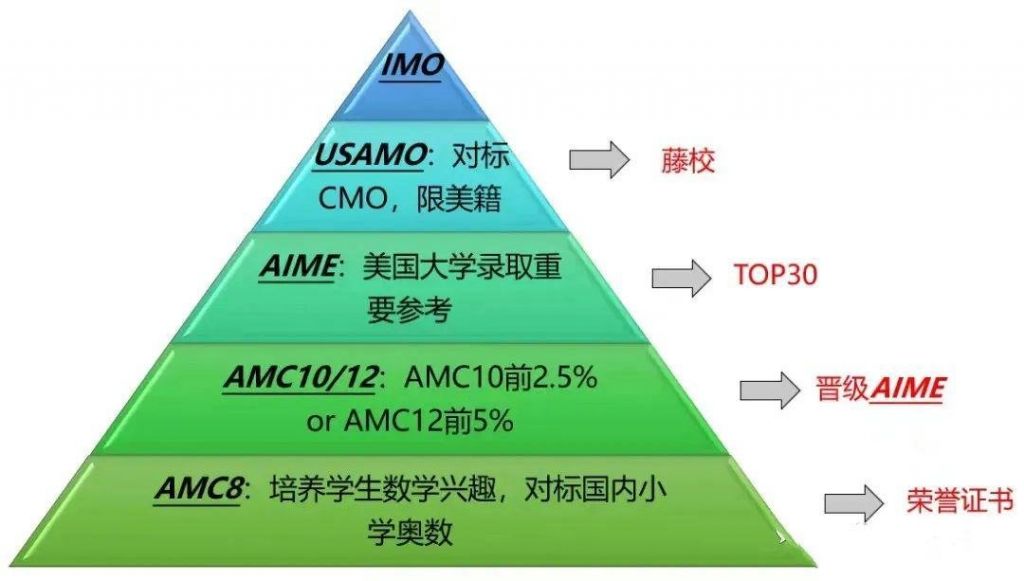
AMC美國(guó)數(shù)學(xué)競(jìng)賽分為三個(gè)等級(jí)，分別是AMC 8，AMC 10，AMC 12，AIME,USAMO\USAJMO，其中，在AMC10和AMC12競(jìng)賽中成績(jī)優(yōu)秀的學(xué)生被邀請(qǐng)參加美國(guó)數(shù)學(xué)邀請(qǐng)賽AIME，AMC和AIME綜合成績(jī)前270名的美國(guó)籍學(xué)生被選入?yún)⒓用绹?guó)奧林匹克數(shù)學(xué)競(jìng)賽USAMO，中國(guó)學(xué)生由于國(guó)籍限制，最終只能晉級(jí)到AIME階段。
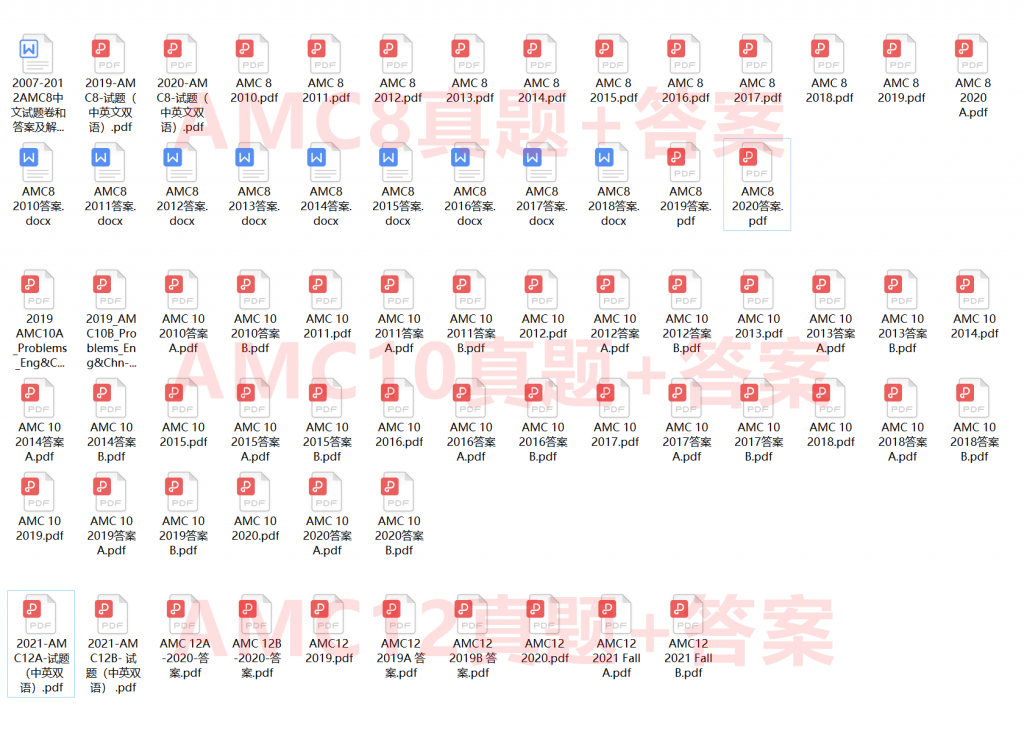
2010年-2022年AMC歷年真題
AMC8/AMC10/AMC12考試規(guī)則
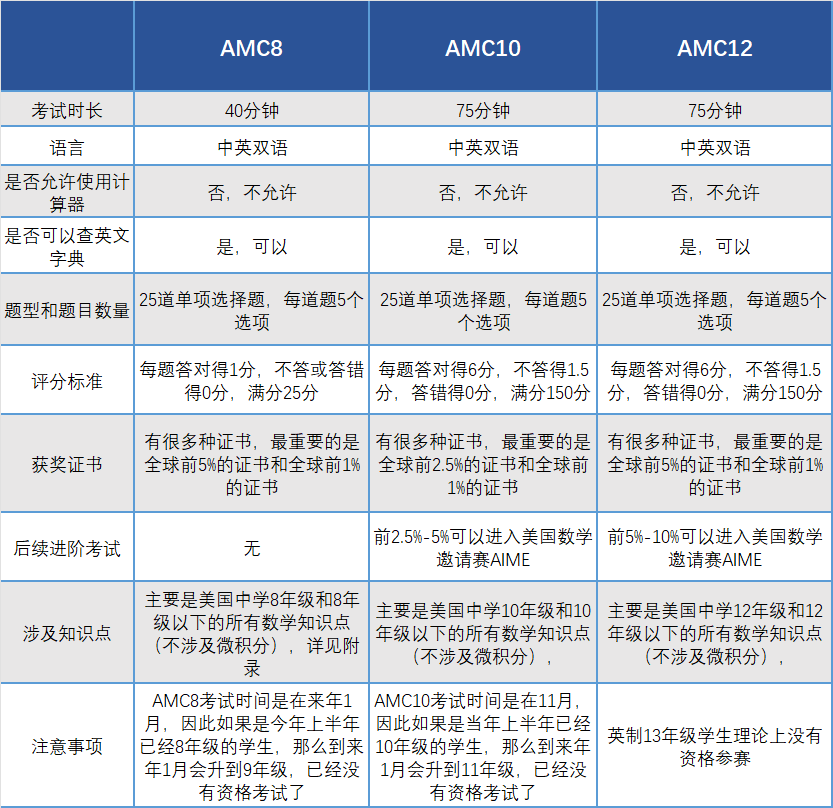
AMC8/AMC10/AMC12在評(píng)分標(biāo)準(zhǔn)也有所不同：AMC8每題答對(duì)得1分，不答或答錯(cuò)得0分，滿(mǎn)分25分；AMC10/AMC12每題答對(duì)得6分，不答得1.5分，答錯(cuò)得0分，滿(mǎn)分150分。
AMC8/AMC10/AMC12區(qū)別還體現(xiàn)在一下多個(gè)方面，具體如圖：
牛娃媽媽-AMC競(jìng)賽上岸經(jīng)驗(yàn)分享
AMC8/10/12 前1%
1. 對(duì)于給孩子的AMC備考，我制定了周密的規(guī)劃。首先花了5個(gè)月的時(shí)間，自主學(xué)習(xí)AMC8/10的知識(shí)點(diǎn)（對(duì)于基礎(chǔ)薄弱或者自學(xué)能力較差的學(xué)生建議從基礎(chǔ)課程開(kāi)始學(xué)習(xí)）。然后，給孩子報(bào)了強(qiáng)化沖刺班上學(xué)習(xí)了兩個(gè)月，培養(yǎng)了孩子在面對(duì)難題時(shí)的數(shù)學(xué)思維能力。孩子說(shuō)在練習(xí)題方面，專(zhuān)業(yè)的教輔材料幫助很大。
2. 核心概念和公式定理一定要熟，建議在學(xué)完每個(gè)知識(shí)點(diǎn)后，在歷年真題中挑出對(duì)應(yīng)的題進(jìn)行專(zhuān)項(xiàng)檢測(cè)，切勿盲目刷題。
3.AMC12比AMC10要難不少，所以我們AMC12是選擇了一對(duì)一，一對(duì)一的老師有時(shí)間根據(jù)孩子的實(shí)際情況制定相應(yīng)的學(xué)習(xí)計(jì)劃，找到孩子思維的漏洞，提升的效果也更顯著。
很多高分的美國(guó)學(xué)生早在小學(xué)就開(kāi)始準(zhǔn)備AMC了。對(duì)國(guó)內(nèi)學(xué)生來(lái)說(shuō)，如果想要在A(yíng)MC比賽中取得好成績(jī)，建議至少提前半年開(kāi)始準(zhǔn)備，蕞好的話(huà)能提前一年開(kāi)始準(zhǔn)備以達(dá)到更好的成果??！
AMC8/AMC10/AMC12備考要點(diǎn)
AMC數(shù)學(xué)競(jìng)賽備考時(shí)，AMC8/AMC10/AMC12競(jìng)賽考察的備考內(nèi)容也不盡相同，難度逐級(jí)遞增。
AMC8競(jìng)賽考點(diǎn)：
基礎(chǔ)代數(shù)：整數(shù)、有理數(shù)、無(wú)理數(shù)、實(shí)數(shù)、數(shù)軸和直角坐標(biāo)系；多元一次方程、簡(jiǎn)單二次方程、簡(jiǎn)單不等式；簡(jiǎn)單數(shù)列；基本代數(shù)技巧。
基礎(chǔ)幾何：基礎(chǔ)幾何作圖；平面歐氏幾何，點(diǎn)、線(xiàn)、三角形、特殊四邊形、圓；規(guī)則圖形的周長(zhǎng)和面積；基本平面幾何技巧；規(guī)則立體幾何圖形。
基礎(chǔ)數(shù)論：奇偶分析、整除的性質(zhì)、最小公倍數(shù)和最大公約數(shù)、同余問(wèn)題。
基礎(chǔ)組合：韋恩圖；排列、組合和概率入門(mén)；階乘和二項(xiàng)式系數(shù)、楊輝三角形。
AMC10競(jìng)賽考點(diǎn)：
進(jìn)階代數(shù)：多項(xiàng)式，余數(shù)定理，韋達(dá)定理，根與系數(shù)的關(guān)系，特殊高次方程；進(jìn)階不等式、均值不等式；函數(shù)入門(mén)，定義域和值域、二次函數(shù)、指數(shù)函數(shù)、對(duì)數(shù)函數(shù)、簡(jiǎn)單三角函數(shù)；數(shù)列進(jìn)階；代數(shù)技巧進(jìn)階。
進(jìn)階幾何：進(jìn)階幾何作圖；三角形進(jìn)階、正弦定理、余弦定理、內(nèi)切圓和外切圓、斯圖瓦爾特定理、共點(diǎn)和共線(xiàn)；圓和四邊形，四點(diǎn)共圓，圓的外切四邊形；正多邊形，角度，周長(zhǎng)和面積；進(jìn)階平面幾何技巧；解析幾何入門(mén)。
立體幾何：點(diǎn)、線(xiàn)、面的關(guān)系，三維坐標(biāo)系；立體幾何作圖；正多面體，歐拉公式；特殊的立體幾何圖形，立體幾何技巧。
進(jìn)階數(shù)論：數(shù)，數(shù)組和序列；模運(yùn)算，復(fù)雜同余問(wèn)題；整數(shù)、分?jǐn)?shù)和小數(shù)，進(jìn)制轉(zhuǎn)換；基本丟番圖方程，進(jìn)階數(shù)論技巧。
進(jìn)階組合：容斥原理；二項(xiàng)式定理及相關(guān)結(jié)論；進(jìn)階排列、組合和概率；期望入門(mén)，遞推、二分法，進(jìn)階組合方法。
AMC12競(jìng)賽考點(diǎn)：
涵蓋所有高中部分的數(shù)學(xué)知識(shí)，在 AMC10 基礎(chǔ)上新增知識(shí)點(diǎn)：
進(jìn)階代數(shù)：復(fù)雜不等式、調(diào)和不等式、輪換不等式、柯西不等式；復(fù)雜函數(shù)問(wèn)題，反函數(shù)和符合函數(shù)，三角函數(shù)和差化積、積化和差，萬(wàn)能公式；復(fù)數(shù)，復(fù)平面，歐拉公式，蒂莫夫公式；數(shù)學(xué)歸納法、復(fù)雜數(shù)列和極限。
進(jìn)階幾何：圓相關(guān)幾何進(jìn)階；數(shù)形結(jié)合，二維、三維圖形的函數(shù)表達(dá)，進(jìn)階解析幾何；不規(guī)則二維、三維圖形的處理；二維向量，三維向量。
進(jìn)階數(shù)論：二次余數(shù)，高次余數(shù)、費(fèi)馬圣誕節(jié)定理、費(fèi)馬小定理；各類(lèi)丟番圖方程的解法。
進(jìn)階組合：隨機(jī)過(guò)程和期望。復(fù)雜組合問(wèn)題技巧。
